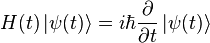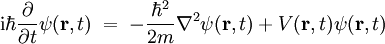سفارش تبلیغ
صبا ویژن

معادله شرودینگر

نوشته شده به وسیله ی ندا جباری در تاریخ 86/12/2:: 12:13 صبح

سلام

این هم از معادله شرودینگر. این مطلب به علت درخواست های مکرر یکی از خوانندگان که به این معادله علاقه عجیبی پیدا کرده بودند گذاشته شده. 

معادله شرودینگر، اساسی‌ترین معادله غیر نسبیتی در مکانیک کوانتومی برای توصیف تحول حالت (state) یک ذره است. معادله شرودینگرتوسط اروین شرودینگر به ثبت رسید و پس از او نیز هایزنبرگ معادله برابری را به صورت عملگرهای خطی و عملگرهای جابجایی به وجود آورد. معادله شرودینگر در حالت ساده به صورت زیر است:

H(t) \left| \psi (t) \right\rangle = i \hbar {\partial\over\partial t} \left| \psi (t) \right\rangle 

در اینجا H یک عملگر خطی در فضای (اصولاً بینهایت بعدی) هیلبرت است و عملگر همیلتونی نام دارد.ویژه مقدارهای این نگاشت اصولاً مقادیر کوانتومی انرژی هستند. ‎ |?>‎، یک بردار در فضایِ هیلبرت است، که حالت ذره را توصیف می‌کند. اگر این بردار را به صورت یک تابع زمان و مکان بنویسیم، معادله شرودینگر چنین حالتی پیدا می‌کند:

\mathrm{i}\hbar\frac{\partial}{\partial t}\psi(\mathbf{r},t) \;=\; - \frac{\hbar^2}{2m}\nabla^2\psi(\mathbf{r},t) + V(\mathbf{r},t)\psi(\mathbf{r},t) 

البته اگر ما ‎|?n>‎ را به عنوان ویژه بردار  H انتخاب کنیم، آن وقت این معادله دیگر متغیر زمانی نخواهد داشت:

H |\psi_n(x)\rang = E_n |\psi_n(x)\rang.  

با در نظر گرفتن نظریه نسبیت خاص، معادله شرودینگر دیگر صادق نیست و در این حالت از معادله دیراک که کلی‌تر است استفاده می‌شود

معادله غیر خطی شرودینگر (Nonlinear Schrdinger equation - NLS) نوع غیر خطی معادله شرودینگر است که در فیزیک نظری کاربرد دارد.
معادله غیر خطی شرودینگر یک معادله دیفرانسیل با مشتقات پاره ای است:

i\partial_t\psi=-{1\over 2}\partial^2_x\psi+\kappa|\psi|^2 \psi 


کلمات کلیدی :

پاسخ